数据结构相关笔记②

W3-W4 的内容

树 (Tree)

在计算机科学中，树是一种抽象的层次结构模型。树结构由节点组成，并且这些节点之间具有父子关系。以下是一些常见的树的术语及其解释：

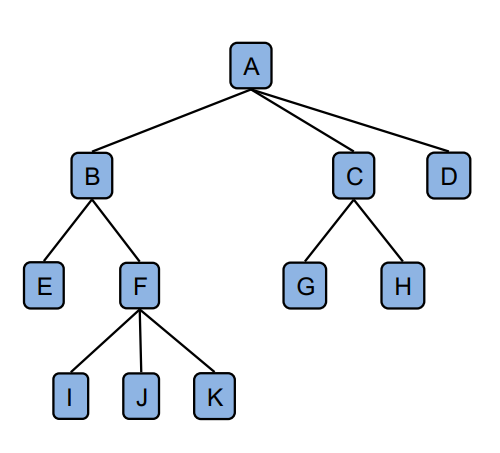
根节点 (Root)

没有父节点的节点。例如，节点 A 是根节点。

内部节点 (Internal Node)

至少有一个子节点的节点。例如，节点 A、B、C 和 F 都是内部节点。

外部节点/叶子节点 (External Node / Leaf Node)

没有子节点的节点。例如，节点 E、I、J、K、G、H 和 D 都是叶子节点。

祖先节点 (Ancestors)

包括父节点、祖父节点、曾祖父节点等。例如，节点 F 的祖先是 A 和 B。

后代节点 (Descendants)

包括子节点、孙节点、曾孙节点等。例如，节点 B 的后代包括 E、F、I、J 和 K。

兄弟节点 (Siblings)

具有相同父节点的两个节点。例如，节点 B 和 D 是兄弟节点。

深度 (Depth)

从根节点到某个节点的路径上的边数。例如，节点 F 的深度为 2。

层级 (Level)

具有相同深度的一组节点。例如，{E, F, G, H} 处于层级 2。

高度 (Height)

树的最大深度。例如，这棵树的高度为 3。

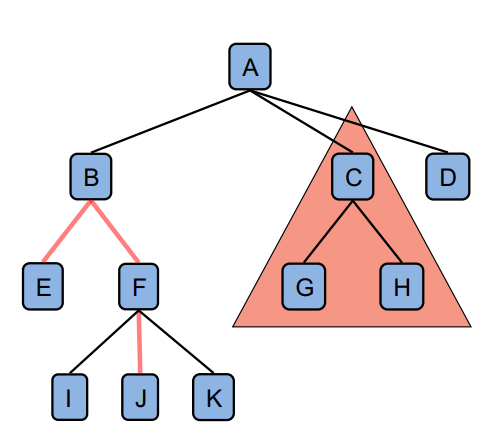
子树 (Subtree)

由某个节点及其所有后代构成的树。例如，以节点 C 为根的子树包括 {C, G, H}。

边 (Edge)

连接两个节点（父节点和子节点）的线段。例如，(B, F) 是一条边。

路径 (Path)

由节点序列构成的，序列中相邻的两个节点有边连接。例如，路径 <E, B, F, J>。

这些术语构成了理解树结构的基础，有助于进一步讨论树的性质和操作。

树的抽象数据类型 (Tree ADT)

树的抽象数据类型（ADT）定义了一组操作和方法，用于操作树结构中的节点。以下是树 ADT 的一些关键操作和方法：

通用方法 (Generic Methods)

integer size()：返回树中节点的数量。
boolean isEmpty()：检查树是否为空。
Iterator iterator()：返回一个用于遍历树的迭代器。
Iterable positions()：返回树中所有节点的位置的集合。

访问方法 (Access Methods)

Position root()：返回树的根节点位置。
Position parent(p)：返回节点 p 的父节点位置。
Iterable children(p)：返回节点 p 的所有子节点位置的集合。
Integer numChildren(p)：返回节点 p 的子节点数量。

查询方法 (Query Methods)

boolean isInternal(p)：检查节点 p 是否为内部节点。
boolean isExternal(p)：检查节点 p 是否为叶子节点。
boolean isRoot(p)：检查节点 p 是否为根节点。

更新方法 (Update Methods)

除了上述基本方法外，某些数据结构实现树 ADT 时还可能定义额外的更新方法，以支持更复杂的操作。

节点对象 (Node Object)

节点对象的实现通常具有以下属性：

value：与该节点关联的值。
children：该节点的子节点集合或列表。
parent：（可选）该节点的父节点。

示例代码

def is_external(v):
    # 检查节点 v 是否为叶子节点
    return v.children.is_empty()

def is_root(v):
    # 检查节点 v 是否为根节点
    return v.parent is None

树的遍历 (Traversing Trees)

树的遍历是指以一种系统的方式访问树中的所有节点。与简单的数据结构（如列表）相比，树的遍历方式更为复杂，存在多种不同的遍历策略。以下是树的主要遍历方式：

先序遍历 (Pre-order Traversal)

口诀：根左右

在先序遍历中，从给定节点开始，首先访问该节点，然后依次访问其子节点。

特点：先访问节点本身，再访问其子节点。
应用：适用于需要在处理子节点之前先处理父节点的情况。

示例代码

def pre_order(v):
    visit(v)  # 对节点 v 进行处理
    for each child w of v:
        pre_order(w)  # 递归遍历子节点

后序遍历 (Post-order Traversal)

口诀：左右根

在后序遍历中，从给定节点开始，首先访问其所有子节点，然后再访问该节点本身。

特点：先访问子节点，再访问节点本身。
应用：适用于需要在处理父节点之前先处理子节点的情况。

示例代码

def post_order(v):
    for each child w of v:
        post_order(w)  # 递归遍历子节点
    visit(v)  # 对节点 v 进行处理

中序遍历 (In-order Traversal)

口诀：左根右

中序遍历仅适用于二叉树。在中序遍历中，从给定节点开始，先访问左子树，然后访问该节点本身，最后访问右子树。

特点：先访问左子树，再访问节点本身，最后访问右子树。
应用：适用于二叉搜索树（BST）等特定情况。

示例代码

def in_order(v):
    if v.left is not None:
        in_order(v.left)  # 递归遍历左子节点
    visit(v)  # 对节点 v 进行处理
    if v.right is not None:
        in_order(v.right)  # 递归遍历右子节点

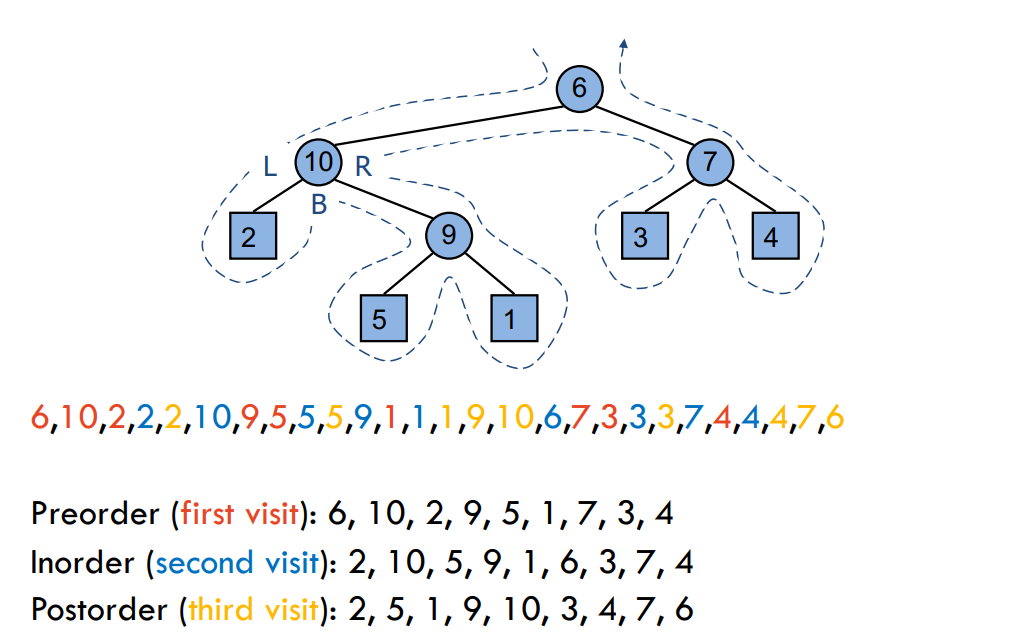
欧拉遍历 (Euler Tour Traversal)

欧拉遍历是一种通用的树遍历方法，适用于二叉树。它结合了先序遍历、中序遍历和后序遍历，是这三种遍历的推广。在欧拉遍历中，遍历者围绕树进行移动，并在每个节点处访问三次：

第一次访问：称为 先序遍历 (Preorder Traversal)。
第二次访问：称为 中序遍历 (Inorder Traversal)。
第三次访问：称为 后序遍历 (Postorder Traversal)。

特点

欧拉遍历可以同时获取先序、中序和后序遍历的结果。
当遍历树时，每个节点会被访问三次：左边一次（先序），底部一次（中序），右边一次（后序）。

树的递归代码示例 (Examples of Recursive Code on Trees)

在树结构中，递归是处理树节点的常用方法。以下是一些常见的递归代码示例，展示了如何通过递归计算树的深度和高度。

计算节点的深度 (Depth of a Node)

节点的深度定义为从根节点到该节点的路径上的边数。根节点的深度为 0。

示例代码

def depth(v):
    # 如果节点 v 是根节点，则深度为 0
    if v.parent is None:
        return 0
    else:
        # 否则，节点 v 的深度为其父节点的深度加 1
        return depth(v.parent) + 1

解释

根节点：如果节点 v 没有父节点（即根节点），那么其深度为 0。
非根节点：如果节点 v 有父节点，那么其深度为父节点深度加 1。

计算树的高度 (Height of a Tree)

节点的高度定义为从该节点到其最深叶子节点的路径上的边数。叶子节点的高度为 0。

示例代码

def height(v):
    # 如果节点 v 是叶子节点（即没有子节点），高度为 0
    if v.isExternal():
        return 0
    else:
        # 计算所有子节点的高度，取最大值并加 1
        h = 0
        for child in v.children:
            h = max(h, height(child))
        return h + 1

解释

叶子节点：如果节点 v 没有子节点（即叶子节点），那么其高度为 0。
非叶子节点：如果节点 v 有子节点，那么计算所有子节点的高度，取最大值并加 1。

递归算法的复杂度分析 (Complexity Analysis of Recursive Algorithms on Trees)

递归算法在树结构上通常具有以下两种复杂度：

遍历所有子节点

最坏情况：对树中的每个节点进行递归调用。
总成本：如果每个节点的工作量是常数，那么总成本与节点数成线性关系，即 O(n)。

遍历单一子节点

最坏情况：每一层递归调用一次。
总成本：如果每层的工作量是常数，那么总成本与树的高度成线性关系，即 O(h)。

示例解释

遍历所有子节点的递归：例如，计算树的高度需要递归调用所有子节点。由于每个节点都被访问一次，所以总成本是 O(n)，其中 n 是节点的总数。
遍历单一子节点的递归：例如，查找最深的节点可能只需要沿着树的一条路径递归。在这种情况下，总成本是 O(h)，其中 h 是树的高度，因为只需在每一层进行一次递归调用。

总结

理解递归算法在树结构上的复杂度分析，对于优化和正确选择算法至关重要。通过分析遍历所有子节点和遍历单一子节点的不同情况，可以更好地预测递归算法的性能表现。