数据结构相关笔记⑥
W7-W8
1.图的基本概念(Graph Basics)
1.1 图的定义
- 图(Graph)是由顶点(Vertices)和边(Edges)组成的一种数据结构。图是一种非线性数据结构,它是由顶点的有穷非空集合和顶点之间边的集合组成的。
1.2 边的类型(Edge Types)
-
有向边(Directed Edge):有向边是一个有序对,它连接两个顶点,其中一个是起始顶点,另一个是终止顶点,有一个箭头指向。
-
无向边(Undirected Edge):无向边是一个无序对,它连接两个顶点,没有起始顶点和终止顶点之分。
1.3 应用场景(Applications)
- 电子电路: 印刷电路板、集成电路。
- 交通网络: 公路网、航线网络。
- 计算机网络: 互联网、网页。
- 建模: 实体关系图、甘特图中的优先关系。
2.图的概念和术语 (Graph Concepts and Terminology)
2.1 路径(Path)
- 定义:路径是图中的一个顶点序列,其中每个顶点都是由边连接到下一个顶点的。
- 简单路径(Simple Path):路径中的顶点不重复。
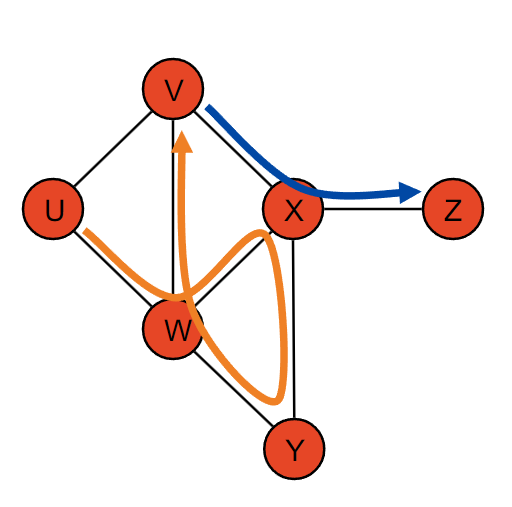
- 示例:(V, X, Z) 是一个简单路径;(U, W, X, Y, W, V) 是一个非简单路径。
2.2 环(Cycle)
- 定义:环是一个简单路径,它的起始顶点和终止顶点相同。
- 简单环(Simple Cycle):环中的顶点不重复,除了起始顶点和终止顶点。
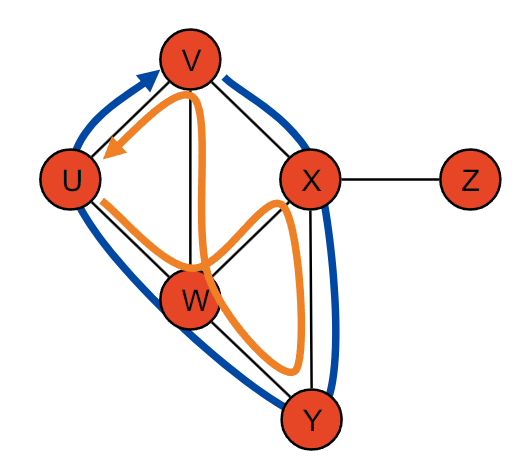
- 示例:(V, X, Y, W, U, V) 是一个简单环;(U, W, X, Y, W, V, U) 是一个非简单环。
2.3 子图(Subgraph)
- 定义:子图是一个图的一部分,它包含图中的一些顶点和边。
- 示例:
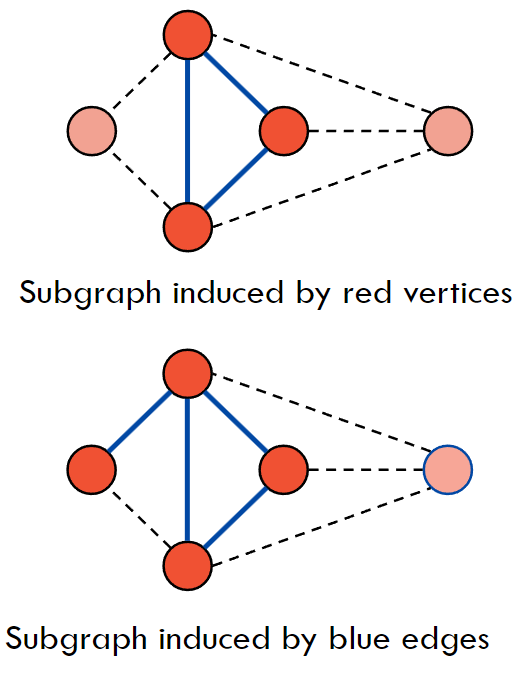
2.4 连通性(Connectivity)
- 定义: 如果图 G 中的每对顶点之间都有路径相连,则图 G 是连通的。
- 连通分量(Connected Component):图 G 的极大连通子图称为 G 的连通分量。
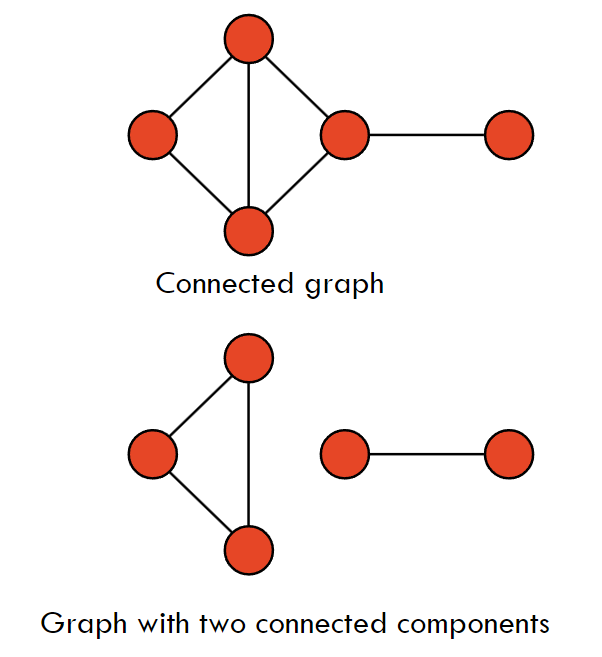
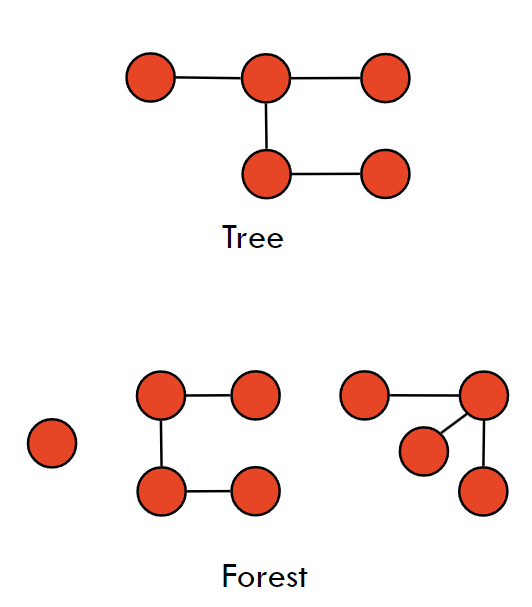
2.5 树和森林(Tree and Forest)
- 树(Tree):一个无环的连通图。
- 森林(Forest):一个或多个树的集合/是一个无环的图,其连通分量都是树。
3.图的数据结构和实现方法(Graph Data Structure)
3.1 抽象数据类型(ADT)方法说明
numVertices():返回图中顶点的数量。numEdges():返回图中边的数量。vertices():返回图中所有顶点的列表。edges():返回图中所有边的列表。getEdge(u, v):返回从顶点 u 到顶点 v 的边。对于无向图,(u, v) 和 (v, u) 是相同的。endVertices(e):返回边 e 的两个顶点的数组/列表。如果是有向图,返回的第一个顶点是起始顶点,第二个顶点是终止顶点。opposite(v, e):返回边 e 的另一个顶点。如果 v 是 e 的一个顶点,则返回 e 的另一个顶点,否则返回错误。outDegree(v):返回顶点 v 出度的数量(从顶点 v 发出的所有边)inDegree(v):返回顶点 v 入度的数量(指向顶点 v 的所有边),对于无向图,入度和出度相同。outgoingEdges(v):返回从顶点 v 出发的所有边的列表。incomingEdges(v):返回指向顶点 v 的所有边的列表,对于无向图,返回的和 outgoingEdges(v) 相同。insertVertex(x):在图中插入一个顶点 x。insertEdge(u, v, x):在顶点 u 和 v 之间插入一条边,储存 x。如果已经存在这条边,则返回错误。removeVertex(v):删除顶点 v 和与之相关的所有边。removeEdge(e):删除边 e。
3.2 边列表 (Edge List)
-
实现方法:使用两个列表,一个存储顶点,一个存储边。
-
顶点序列(Vertex Sequence):顶点的列表。
-
顶点对象(Vertex Object):包含顶点的数据和指针。
-
边序列(Edge Sequence):边的列表。
-
边对象(Edge Object):每个边对象指向它连接的两个顶点。
-
示例:一个简单的无向图,包含四个顶点(u, v, w, z)和四条边(e, f, g, h)。
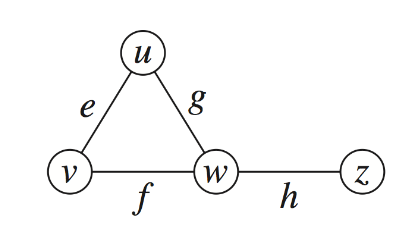
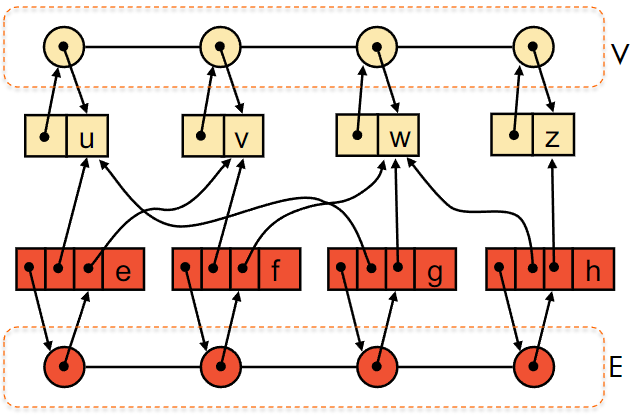
顶点序列 (V) 包含所有顶点对象。
边序列 (E) 包含所有边对象,每个边对象都指向它所连接的两个顶点。
3.3 领接表 (Adjacency List)
-
定义:对于每个顶点 v,存储一个包含所有与 v 相关的边的列表。每个顶点(如 u, v, w)维护一个与其相关的边的序列。这个序列包含了所有连接到该顶点的边。对于每个边对象,存储它连接的两个顶点。
-
示例:一个简单的无向图,有三个顶点 (u, v, w) 和两条边 (a, b)。
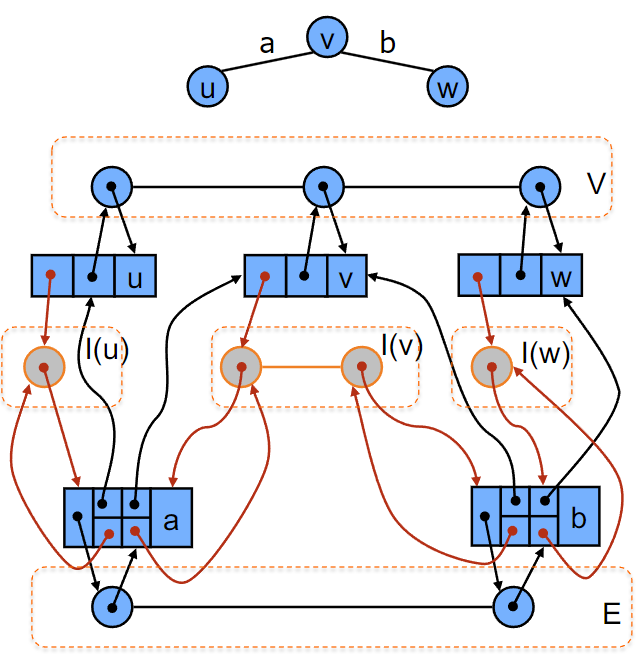
每个顶点维护一个与其相连的边的列表(例如,顶点 v 维护边 a 和 b 的列表)。
每个边对象(例如 a 和 b)指向与其连接的顶点,并在相应的顶点序列中记录它们的位置。
3.4 领接矩阵 (Adjacency Matrix)
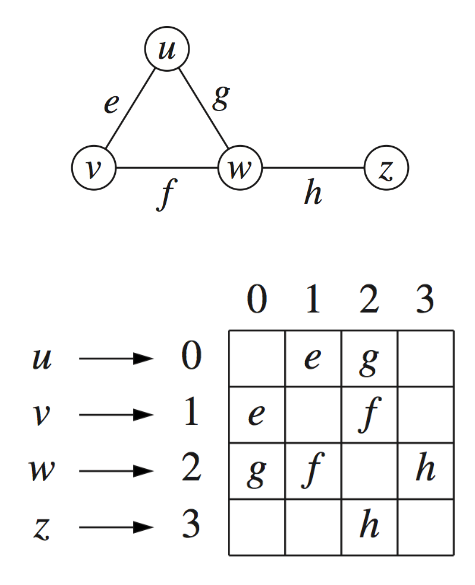
- 顶点数组 (Vertex Array)
将每个顶点分配一个从 0 到 n-1 的唯一索引,其中 n 是图中的顶点数量。
顶点 u 被分配了索引 0,v 是 1,w 是 2,z 是 3。
- 二维数组表示 (2D-Array Adjacency Matrix)
使用一个二维数组(矩阵)A 来表示图的邻接关系。矩阵的大小为 𝑛×𝑛,其中 𝑛 是顶点的数量。
如果顶点 i 和顶点 j 之间存在边,则 A[i][j] 存储该边的引用(或者对于无权图来说是一个标志,例如 1 或 true)。
如果顶点 i 和顶点 j 之间没有边,则 A[i][j] 为 null 或 0。
邻接矩阵的特点:
边的引用(Reference to Edge Object):
对于相邻的顶点(例如 u 和 v 之间的边 e),矩阵中对应位置存储边对象的引用。
空值(Null for Nonadjacent Vertices):
对于不相邻的顶点,矩阵中对应位置为 null,表示没有边连接这两个顶点.
对比
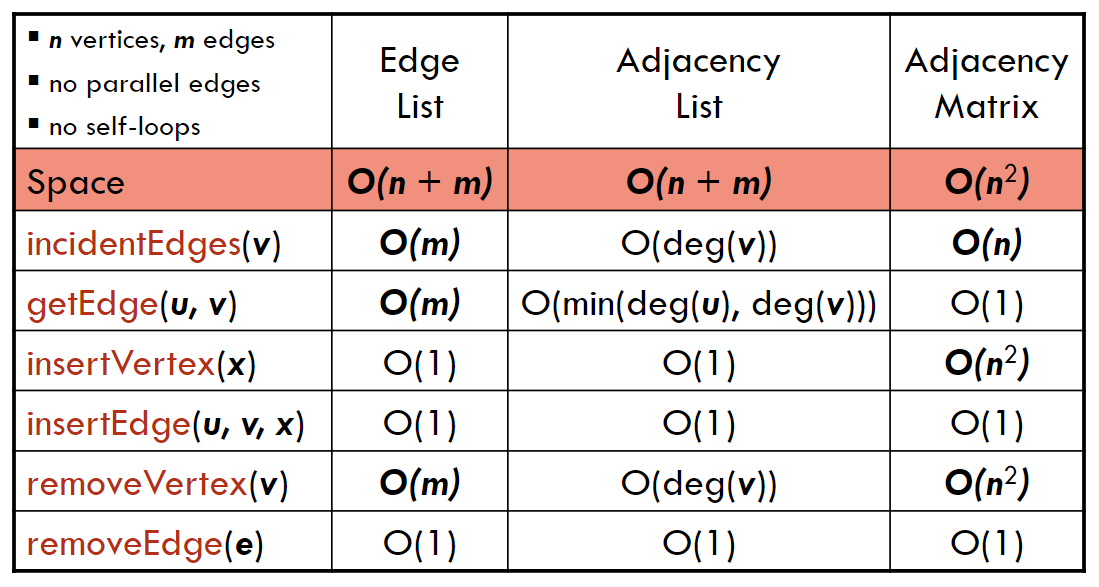
4.图的遍历(Graph Traversal)
4.1 深度优先搜索(Depth-First Search, DFS)
-
定义:从一个起始顶点开始,沿着一条路径一直走到不能走为止,然后返回到上一个顶点,继续走下一条路径,直到所有的路径都走完。
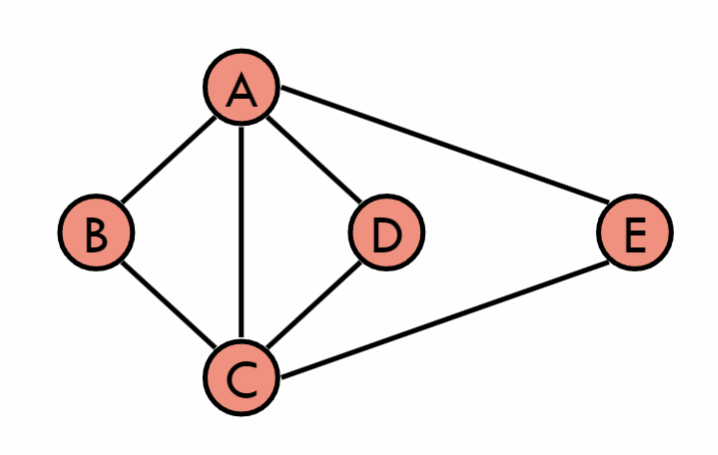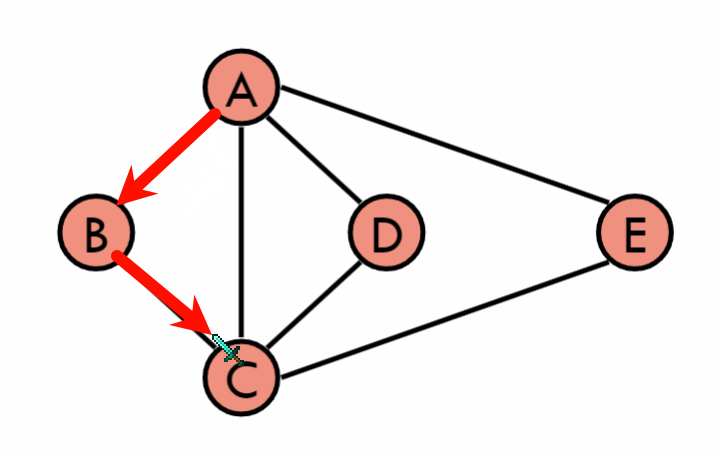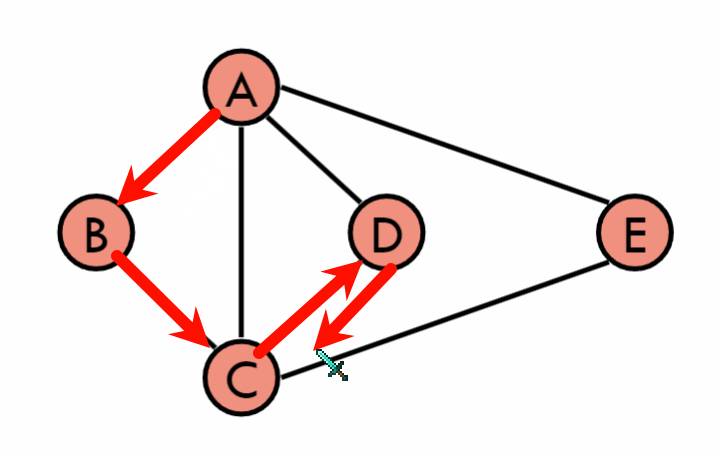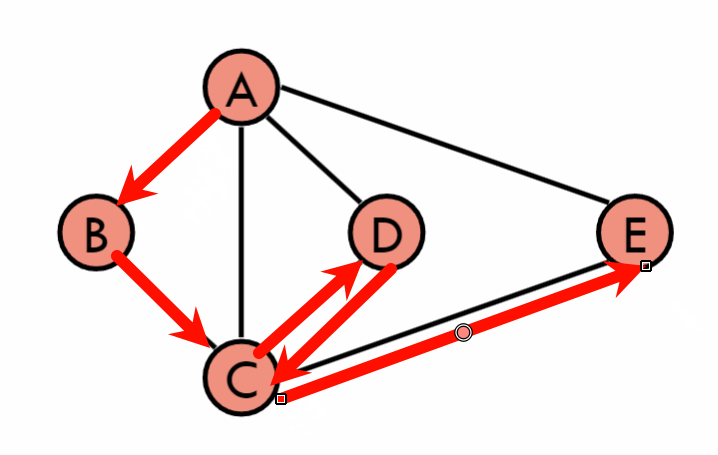
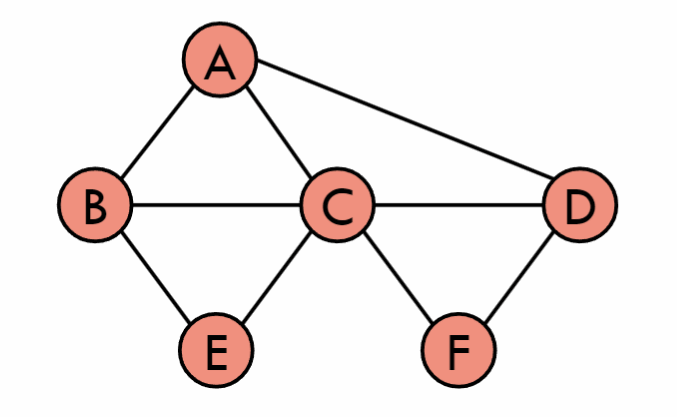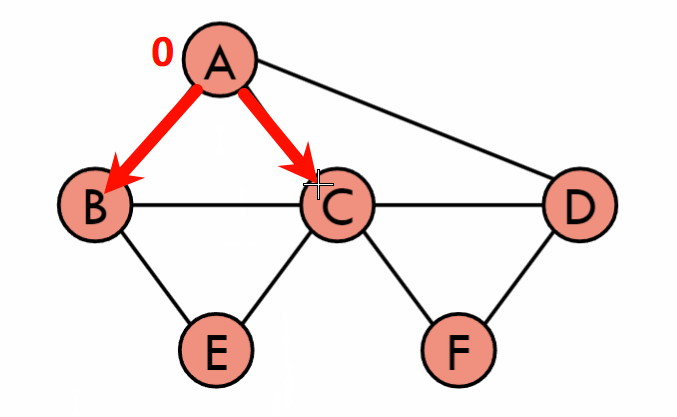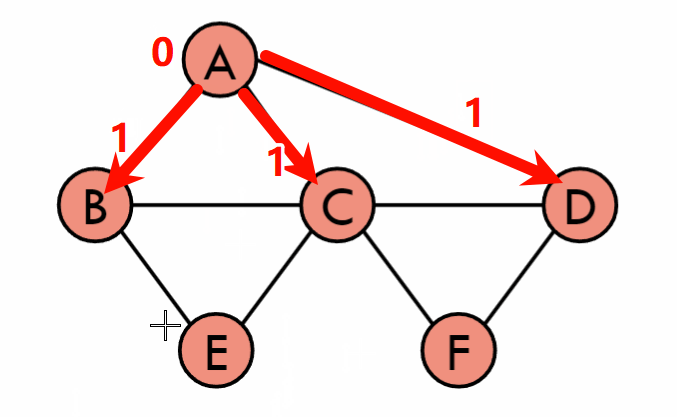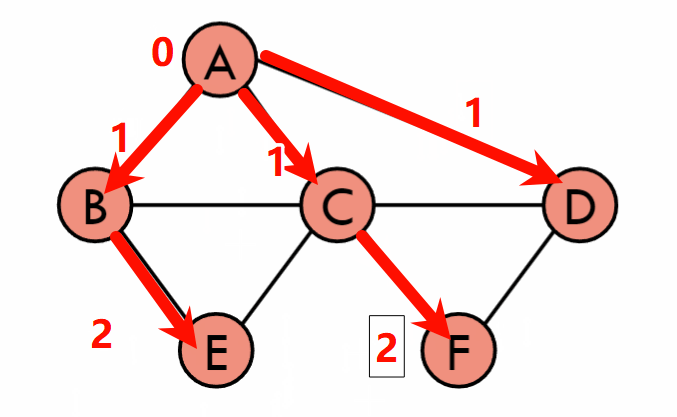
4.2 广度优先搜索(Breadth-First Search, BFS)
-
定义:从一个起始顶点开始,先访问起始顶点的所有邻居,然后再访问邻居的邻居,依次类推。