数据结构相关笔记⑦

W9

1. 数据结构相关笔记①
2. 数据结构相关笔记②
3. 数据结构相关笔记③
4. 数据结构相关笔记④
5. 数据结构相关笔记⑤
6. 数据结构相关笔记⑥
7. 数据结构相关笔记⑦

贪心算法（Greedy Algorithm）

• 定义：贪心算法是一类算法，解决问题时每一步都选择当前状态下的局部最优解，希望通过这样的选择可以找到全局最优解。
• 特点：贪心算法的每一步都选择当前状态下的局部最优解，而不考虑全局最优解，因此贪心算法通常比较简单，容易实现。

1.贪心算法的通用形式

def generic_greedy(input):
# 初始化
  initialize result
# 这里可以对输入进行排序，以确定考虑输入的顺序
  determine order in which to consider input

# 迭代选择贪心解
  for each element i of the input (in above order) do
# 如果元素 i 改进了结果，则更新结果
    if element i improves result then
      update result with element i
  return result

2.分数背包问题 (Fractional Knapsack Problem)

• 问题描述：给定一组物品，每个物品有两个属性

  • b[i]：物品的价值
  • w[i]：物品的重量
  • 目标是选择若干物品，使得总效益最大，并且总重量不超过给定的限制 W。

• 贪心策略：按照物品的 效益/重量比值（即单位重量的效益）从高到低的顺序依次选择物品，直到背包达到最大容量。

• 算法实现：

def fractional_knapsack(b, w, W):
  # 把物品的benefit放到数组中
  x ← array of size |b| of zeros
  # 初始化当前weight
  curr ← 0

  while curr < W do:
    # 拿最好的还没有被选择的物品（可以有以下三种）
    i ← "best" item not yet chosen
    # 如果物品i的重量小于剩余的weight，那么就拿全部，不是就只拿一部分，填满剩余的weight
    x[i] ← min(w[i], W - curr)
    # 更新当前weight
    curr ← curr + x[i]
  return x

复杂度分析：
需要 $O(n \log n)$ 来排序物品，在循环内处理物品需要 $O(n)$ .

• 效益优先：选择效益最高的物品。
  
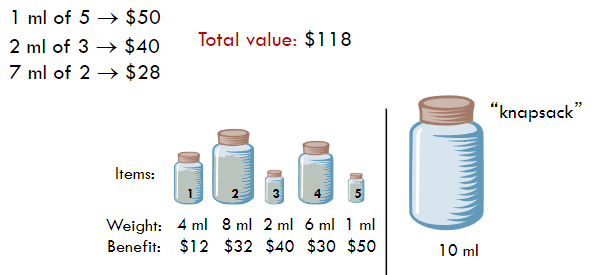
• 重量优先：选择重量最轻的物品。
  
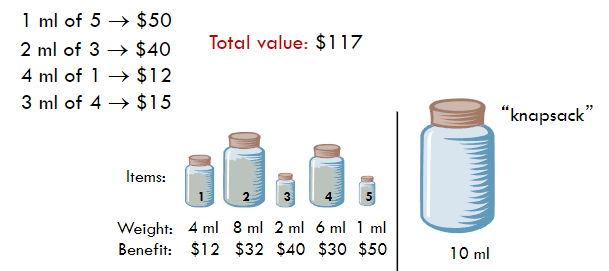
• 效益/重量比优先：选择效益/重量比最高的物品。
  

3.任务调度问题 (Task Scheduling Problem)

• 问题描述：给定 n 个讲座，每个讲座有一个开始时间 s 和结束时间 f。目标是使用最少的教室安排所有讲座，使得没有两个讲座在同一教室内同时进行。
  

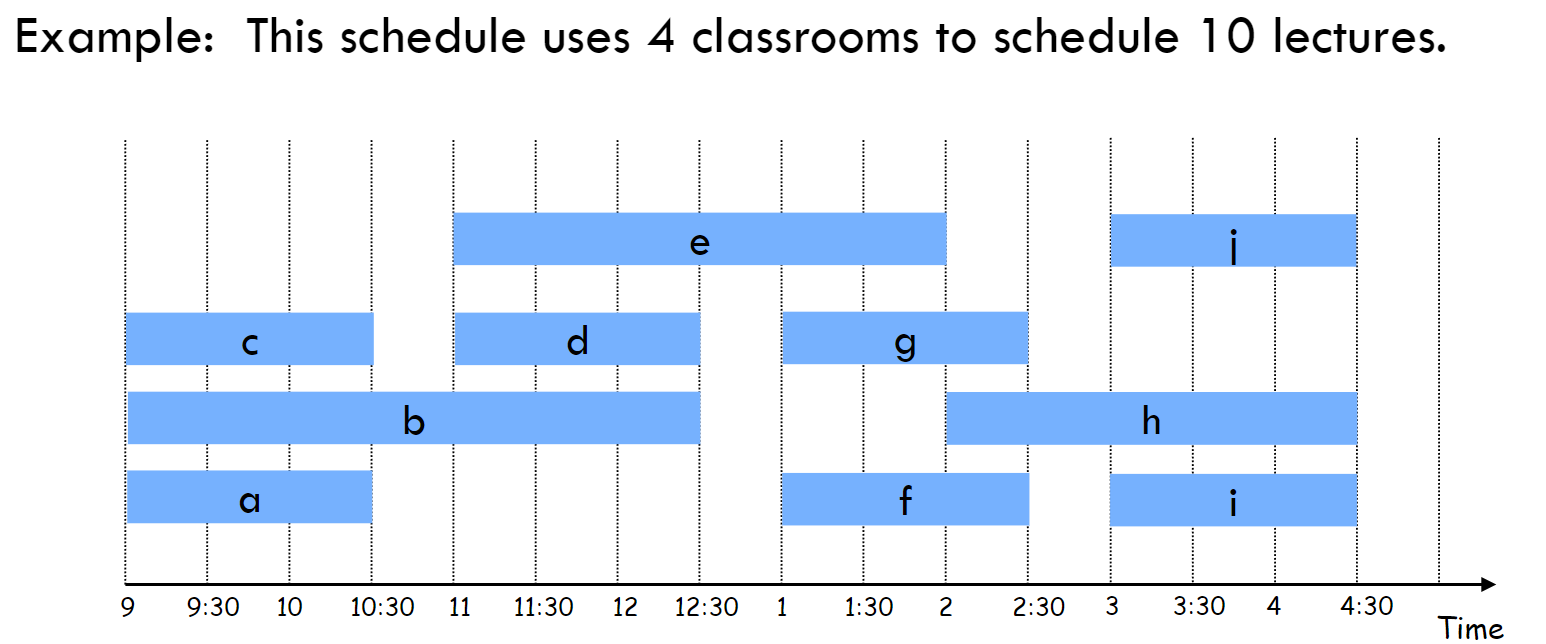
• 贪心策略：使用分区间的贪心策略 Interval Partitioning: Lower bound（区间划分：下限），按照结束时间从早到晚的顺序安排讲座。

• 算法实现：

def interval_partition(S):
  # 按照开始时间排序
  sort intervals in increasing starting time order
  d ← 0    # 已分配的教室数量

  # 逐个分配教室
  for i in increasing starting time order do:
    # 如果讲座 i 与某个教室兼容，则安排在该教室
    if lecture i is compatible with some classroom k:
      # 安排在教室 k
      schedule lecture i in classroom 1 ≤ k ≤ d
    # 如果讲座 i 与所有教室都不兼容，则分配一个新的教室
    else:
      # 分配一个新的教室
      allocate a new classroom d+1
      schedule lecture i in classroom d+1
      d ← d+1
  return d

复杂度分析：需要 $O(n \log n)$ 解法如下：

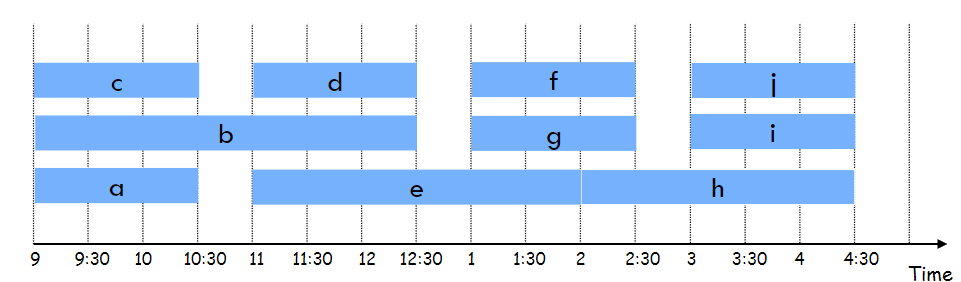
4.哈夫曼编码 (Huffman Encoding)

• 介绍：哈夫曼编码是一种基于贪心策略的编码方法，它的目标是给出现频率高的字符分配短的编码，给出现频率低的字符分配长的编码，从而让整体编码长度最短。

4.1 前缀编码 (Prefix Codes)

• 定义：前缀码是一种特殊的编码方式，保证任何字符的编码都不会是其他字符编码的前缀。

• 例子：例如，假设字符 A 的编码是 0，字符 B 的编码是 10，字符 C 的编码是 110，这是一种前缀码编码，因为没有任何字符的编码是另一个字符编码的前缀。
  

• 频率越高，编码越短：高频字符应该用较短的二进制码来表示，低频字符用较长的编码表示，这样可以确保整体编码的长度最短。

4.2 哈夫曼编码的步骤

• 1.计算字符频率：首先，统计给定字符串中每个字符的频率。频率越高的字符，我们希望它的编码越短。

• 2.创建节点：为每个字符创建一个节点，节点的权值为该字符的频率。

• 3.构建哈夫曼树：构建哈夫曼树，每次从所有节点中选择两个最小的节点，将它们合并为一个新的节点，新节点的权值是两个原节点权值之和。这个合并过程会一直重复，直到只剩下一个节点，这个节点就是哈夫曼树的根节点。

• 4.生成编码：从根节点开始，对哈夫曼树进行深度优先搜索，每次向左走编码为 0，向右走编码为 1，直到叶子节点。叶子节点的路径就是字符的编码。

4.3 哈夫曼编码的详细算法

def huffman(C, f):
    # 初始化优先队列 Q，存储每个字符和它的频率
    Q ← empty priority queue
    for c in C:  # 遍历字符集合
        T ← single-node binary tree storing c  # 为每个字符创建单节点树
        Q.insert(f[c], T)  # 将字符的频率和树插入队列

    # 合并树的过程
    while Q.size() > 1:
        f1, T1 ← Q.remove_min()  # 移除频率最小的两棵树
        f2, T2 ← Q.remove_min()
        # 创建新树，将T1和T2作为左右子树
        T ← new binary tree with T1/T2 as left/right subtrees
        f ← f1 + f2  # 新树的频率是T1和T2的频率之和
        Q.insert(f, T)  # 将新树插入队列

    # 最后剩下的树就是哈夫曼树
    f, T ← Q.remove_min()
    return T  # 返回哈夫曼树

4.4 哈夫曼算法的时间复杂度

• 1.构建哈夫曼树的时间复杂度
  构建哈夫曼树的关键操作是不断从优先队列（优先级队列）中取出两个最小的元素，并将它们合并，然后将新生成的节点插回优先队列中。
  • 初始化优先队列：给定一个包含 d 个不同字符的集合，我们需要将这些字符和它们的频率插入到优先队列中。初始化优先队列的操作需要$O(d)$次操作。如果优先队列是用堆来实现的，那么插入一个元素的时间复杂度是 $O(\log d)$，因此初始化优先队列的时间复杂度是 $O(d \log d)$。
  • 合并节点：在每次迭代中，我们需要从优先队列中取出两个最小的节点，然后将它们合并为一个新的节点。这个操作需要 $O(\log d)$ 的时间。因为我们需要合并 $d-1$ 次，所以合并节点的时间复杂度是 $O((d-1) \log d)$，总的时间复杂度是 $O(d \log d)$。
• 2.生成编码的时间复杂度
  在构建完哈夫曼树之后，接下来的任务是对每个字符生成对应的哈夫曼编码。生成编码的复杂度取决于字符串的长度 n 和字符集的大小 d。
  • 生成编码：对于每个字符，我们需要沿着哈夫曼树从根节点走到叶节点，生成该字符的编码。生成一个字符编码的时间复杂度是与该字符在哈夫曼树中的深度成正比的。总的编码时间可以表示为所有字符的频率乘以它们在哈夫曼树中的深度的和。这个和可以用以下公式表示：

    $$\sum_{c \in C} f[c] \cdot d[c]$$

    其中，$f[c]$ 是字符 c 的频率，$d[c]$ 是字符 c 在哈夫曼树中的深度。因此，生成编码的时间复杂度是 $O(n)$。
• 3.总的时间复杂度
  综上所述，构建哈夫曼树的时间复杂度是 $O(d \log d)$，生成编码的时间复杂度是 $O(n)$。因此，哈夫曼算法的总时间复杂度是 $O(d \log d + n)$。其中，d 是不同字符的数量（字符集的大小），n 是字符串的长度（字符总数）。

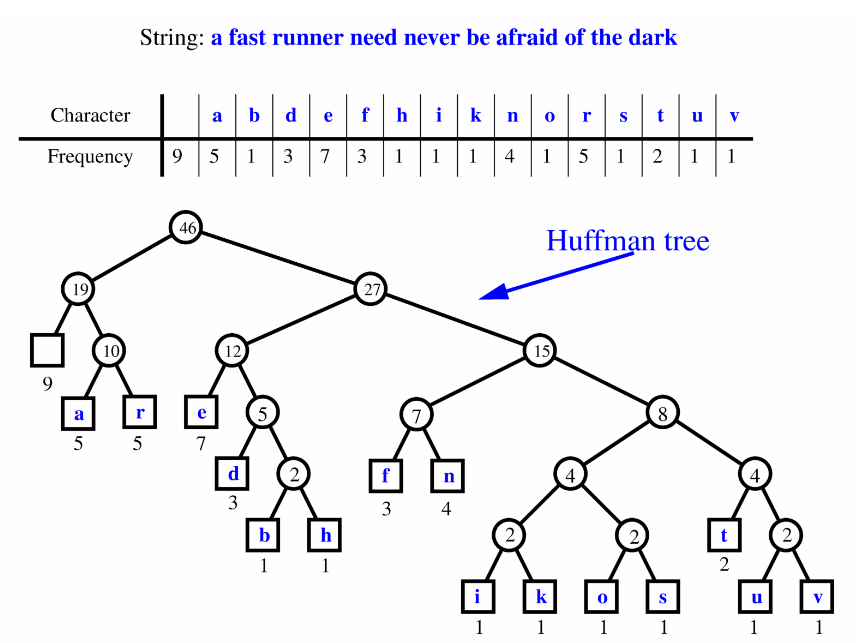
4.5 示例：构建哈夫曼树