数据结构相关笔记④

优先队列 (Priority Queue)

定义：优先队列是一种抽象数据类型，支持插入元素和删除最大（最小）元素的操作。优先队列的元素具有优先级，每次删除操作都会删除优先级最高的元素。
操作方法：
- insert(k, v)：插入键为 k，值为 v 的项。
- remove_min()：删除并返回具有最小键的项。
- min()：返回具有最小键的项但不删除。
- size()：返回队列中存储的项数。
- is_empty()：检查队列是否为空。

优先队列的实现方法

基于无序序列的优先队列 (Unsorted List Implementation)

插入操作 (insert)：时间复杂度为 O(1)，可以将项插入序列的开头或结尾。
删除最小项和查找最小项 (remove_min and min)：时间复杂度为 O(n)，因为必须遍历整个列表以找到最小的键。

基于有序序列的优先队列 (Sorted List Implementation)

插入操作 (insert)：时间复杂度为 O(n)，需要找到适合插入的位置。
删除最小项和查找最小项 (remove_min and min)：时间复杂度为 O(1)，最小项总是位于列表的开头。

优先队列排序 (Priority Queue Sorting)

步骤

逐个将键插入到空的优先队列中。
逐个调用 remove_min() 以获取按顺序排列的键。

复杂度分析

n 次插入操作。
n 次 remove_min() 操作。
对于基于序列的实现方法，总时间复杂度为 O(n²)。

选择排序 (Selection Sort)

选择排序的原理：
- 通过无序序列的优先队列实现。
- 插入 n 个元素需要 O(n) 时间。
- 删除 n 个元素需要 O(n²) 时间。
选择排序的特点：
- 可以原地进行，不需要额外空间。

伪代码：

def selection_sort(A):
    n = len(A)
    for i in range(n):
        # 找到最小的元素
        s = i
        for j in range(i, n):
            if A[j] < A[s]:
                s = j
        # 交换A[i]和A[s]
        A[i], A[s] = A[s], A[i]

插入排序 (Insertion Sort)

插入排序的原理：
- 通过有序序列的优先队列实现。
- 插入 n 个元素需要 O(n²) 时间。
- 删除 n 个元素需要 O(n) 时间。

伪代码：

def insertion_sort(A):
    n = len(A)
    for i in range(1, n):
        x = A[i]
        # 将大于x的元素向前移动
        j = i
        while j > 0 and A[j-1] > x:
            A[j] = A[j-1]
            j -= 1
        A[j] = x

堆 (Heap)

堆的定义：

堆是一种二叉树，用于存储键-值对，并满足以下两个性质：

堆序性质 (Heap-Order Property)：每个节点的键大于等于其父节点的键。
完全二叉树 (Complete Binary Tree)：除了最后一层，其余所有层都是满的，最后一层的节点从左至右填充。

堆排序 (Heap Sort)：

使用堆实现优先队列排序，时间复杂度为 O(nlogn)。

插入到堆 (Insertion into a Heap)：

上浮操作 (Upheap)：插入新节点后，通过向上交换恢复堆序性质。时间复杂度为 O(logn)。

从堆中删除最小项 (Remove Min from a Heap)：

下沉操作 (Downheap)：删除根节点后，通过向下交换恢复堆序性质。时间复杂度为 O(logn)。

优先队列 (Priority Queue)

优先队列的实现方法

基于无序序列的优先队列 (Unsorted List Implementation)

基于有序序列的优先队列 (Sorted List Implementation)

优先队列排序 (Priority Queue Sorting)

步骤

复杂度分析

选择排序 (Selection Sort)

插入排序 (Insertion Sort)

堆 (Heap)

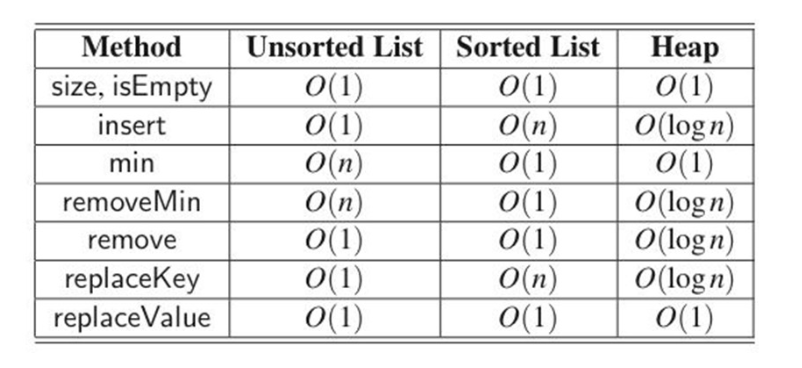
总结